O Rodrigue G

Un amplificateur opérationnel (aussi dénommé ampli-op ou ampli
op, AO, AOP, ALI ou AIL) est un amplificateur différentiel : c'est
un amplificateur électronique qui amplifie une différence de
potentiel électrique présente à ses entrées. Les applications de l'amplificateur opérationnel sont divisées en
deux grandes catégories suivant la nature de la contre-réaction :

Si elle s'opère sur l'entrée inverseuse, la contre-réaction est dite négative ce qui engendre un fonctionnement du système en mode linéaire.

Si elle s'opère sur l'entrée non inverseuse, la contre-réaction est
dite positive et a tendance à accentuer l'instabilité de la sortie qui part vers l'une des tensions de saturation. Le fonctionnement est
alors en mode comparateur.

1-Circuits en mode linéaire

1-1-L'amplificateur suiveur

$V_mathrm{s} = V_mathrm{e} !$

$Z_mathrm{e} = infin$

Souvent appelé Étage tampon de tension (Buffer en anglais). Grâce à son impédance d'entrée très importante et à sa faible impédance de sortie, il est destiné à permettre l'adaptation d'impédance entre deux étages sucessifs d'un circuit.

Démonstration

1-2-L'amplificateur inverseur

Démonstration

Supposons que l'amplificateur opérationnel soit parfait, nous pouvons alors affirmer que $i + = i - = 0$ .
Nous constatons qu'il y a aussi une contre réaction négative (liaision physique entre sortie et entrée inverseuse), donc l'étude se fait en mode linéaire, ce qui engendre $V ed = 0$ et $V + = V -$ .
Nous pouvons affirmer que $V + = 0$ et d'après le théorème de Millman :       $V^- = {left ({V_mathrm{e} over R_mathrm{1}} + {V_mathrm{s} over R_mathrm{2}} right) over {{1 over R_mathrm{1}} + {1 over R_mathrm{2}}} }$ .
Or, comme $V + = V -$ on a :          $0 = left ({V_mathrm{e} over R_mathrm{1}} + {V_mathrm{s} over R_mathrm{2}} right)$ .
Donc                    $V_mathrm{s} = - V_mathrm{e} left ( {R_mathrm{2} over R_mathrm{1}} right)$

1-3-L'amplificateur non inverseur

Démonstration

Supposons que l'amplificateur opérationnel soit parfait, nous pouvons alors affirmer que $i + = i - = 0$ .
Nous constatons qu'il y a aussi une contre réaction négative (liaison physique entre sortie et entrée inverseuse), donc l'étude se fait en mode linéaire, ce qui engendre $V ed = 0$ et $V + = V -$ .
Par technique de superposition sur l'entrée inverseuse de l'amplificateur opérationnel, nous pouvons en déduire que $V_mathrm{e} left ( R_1 + R_2 right) = 0R_2 + R_1V_mathrm{s}$
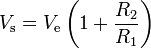
Donc $V_mathrm{s} = V_mathrm{e} left ( 1 + {R_2 over R_1} right)$

1-4-L'amplificateur différentiel

La sortie est proportionnelle à la différence des signaux appliqués aux deux entrées.

$V_mathrm{s} = V_2 left( { left( R_mathrm{f} + R_1 right) R_mathrm{g} over left( R_mathrm{g} + R_2 right) R_1} right) - V_1 left( {R_mathrm{f} over R_1} right)$

Quand $R 1 = R 2$ et $R f = R g$ , $V_mathrm{s} = {R_mathrm{f} over R_1} left( V_2 - V_1 right)$ Quand $R 1 = R 2 = R f = R g$ , $V_mathrm{s} = V_2 - V_1 ,!$

1-5-L'amplificateur sommateur inverseur

Additionne plusieurs entrées pondérées

$V_mathrm{s} = - R_mathrm{f} left( { V_1 over R_1 } + { V_2 over R_2 } + cdots + {V_n over R_n} right)$

Quand $R_1 = R_2 = cdots = R_n$

$V_mathrm{s} = - left( {R_mathrm{f} over R_1} right) (V_1 + V_2 + cdots + V_n ) !$

Quand $R_1 = R_2 = cdots = R_n = R_mathrm{f}$

$V_mathrm{s} = - ( V_1 + V_2 + cdots + V_n ) !$

La sortie est inversée
L'impédance d'entrée $Z n = R n$ , pour chaque entrée ( $V -$ est une masse vituelle)

1-6-Montage intégrateur

La sortie est proportionnelle à l'intégrale temporelle de la tension d’entrée.

$V_mathrm{s}(t) = - left ({1 over RC} right)int {V_mathrm{e}(t)dt}$

En ajoutant une résistance aux bornes du condensateur, on obtient le schéma d’un filtre passe-bas.

Démonstration

Supposons que l'amplificateur opérationnel soit parfait, nous pouvons alors affirmer que $i + = i - = 0$ et que $V + = V - = 0$ . Le courant $I$ traversant R et C est donné par:

$I(t) = frac{V_e(t)}{R}$

Il peut aussi être exprimé en fonction de la tension de sortie :

$I(t) = - C frac{dV_mathrm{s}(t)}{dt}$

En utilisant les deux équations précédentes on obtient :

$V_mathrm{s}(t) = - left ({1 over RC} right)int {V_mathrm{e}(t)dt}$

1-7-Montage dérivateur

La sortie est proportionnelle au taux de variation de la tension d’entrée.

$V_mathrm{s}(t) = - RC frac{dV_mathrm{e}(t)}{dt}$

Le dérivateur est utilisé dans les systèmes de régulation pour surveiller le taux de variation de grandeurs physiques telles que par exemple la température ou la pression.
En ajoutant une résistance en série avec le condensateur, on obtient le schéma d’un filtre passe-haut.

Démonstration

Supposons que l'amplificateur opérationnel soit parfait, nous pouvons alors affirmer que $i + = i - = 0$ et que $V + = V - = 0$ . Le courant $I$ traversant R et C est donné par:

$I(t) = -frac{V_s(t)}{R}$

Il peut aussi être exprimé en fonction de la tension de sortie :

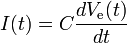
$I(t) = C frac{dV_mathrm{e}(t)}{dt}$

En utilisant les deux équations précédentes on obtient :

$V_mathrm{s}(t) = - RC frac{dV_mathrm{e}(t)}{dt}$

2-Circuits en mode non-linéaire

2-1-Comparateur

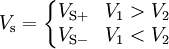
$V_mathrm{s} = left{begin{matrix} V_mathrm{S+} & V_1 > V_2 V_mathrm{S-} & V_1 < V_2 end{matrix}right.$

2-2-Comparateur à deux seuils ou Trigger de Schmitt

2-2-1-Comparateur à deux seuils non inverseur

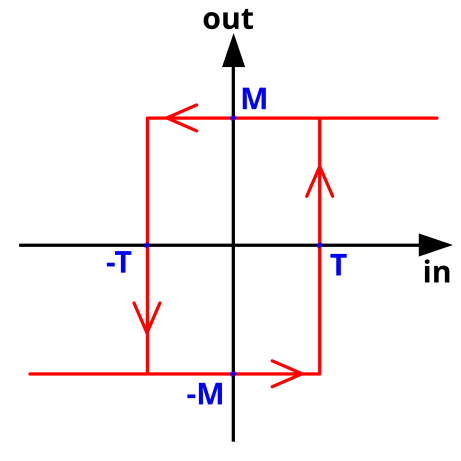
Tension de basculement positif : $V_mathrm{T^+} = V_mathrm{cc} left ( {R_1 over R_2} right)$
Tension de basculement négatif : $V_mathrm{T^-} = - V_mathrm{cc} left ( {R_1 over R_2} right)$
T pour threshold, signifiant seuil.

Note : remarquez la position des entrées inverseuse et non-inverseuse par rapport au montage amplificateur-inverseur.

Démonstration

Pour cette étude, on considérera que l'amplificateur opérationnel utilisé est parfait, et qu'il fonctionne en « mode comparateur » car il utilise une contre-réaction sur l'entrée non-inverseuse de l'AOP. Le gain différentiel de l'amplificateur étant infini, la tension de sortie V_s ne peut valoir que +V_cc ou -V_cc suivant le signe de la tension différentielle V_diff.

$V_{diff}=V_+-V_-=V_+=V_e cdot frac{R_2}{R_1+R_2} + V_s cdot frac{R_1}{R_1+R_2}$

La tension V_e annulant la tension différentielle V_diff vaut donc :

$V_e =-V_s cdot frac{R_1}{R_2}$

Suivant le signe de V_s, on peut définir une tension de basculement positif V_T⁺ faisant passer la sortie V_s de -V_cc a +V_cc, et une tension de basculement négatif V_T^- faisant passer V_s de +V_cc a -V_cc :

Tension de basculement positif : $V_mathrm{T^+} = V_mathrm{cc} left ( {R_1 over R_2} right)$
Tension de basculement négatif : $V_mathrm{T^-} = - V_mathrm{cc} left ( {R_1 over R_2} right)$

2-2-2-Comparateur à deux seuils inverseur

Tension de basculement positif : $V_mathrm{T^+} = V_mathrm{cc} left ( {R_1 over R_1 + R_2} right)$
Tension de basculement négatif : $V_mathrm{T^-} = - V_mathrm{cc} left ( {R_1 over R_1 + R_2} right)$
T pour threshold, signifiant seuil.

Démonstration

$V_{diff}=V_+-V_-=V_+=V_s cdot frac{R_1}{R_1+R_2}-V_e$

La tension V_e annulant la tension différentielle V_diff vaut donc :

$V_e =V_s cdot frac{R_1}{R_1+R_2}$