|
Condensateur
Inductance
Buzzer et Piezo
Diode
Transistor
Composants Passifs_Résistance
La résistance est surement le composant le plus répandu. Certains l'appelle résistor, ou encore plus rarement résisteur.
Son symbole électronique est le suivant:
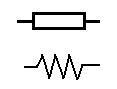
La valeur de ce composant est appelée aussi résistance et est donnée en Ohm. Cette valeur peut être déterminée par le code de couleur pour les composants traditionnels, et simplement lue sur le boîtier des composants CMS.
La valeur de 2 résistances en série est égale à :
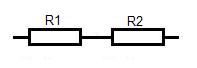
Req=R1+R2
Si on place 2 résistances en parallèles:

1/Req=1/R1+1/R2
Potentiomètre
Un potentiomètre n'est autre qu'une résistance ajustable.
Son symbole électronique est le suivant:
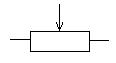
Il possède 3 pattes ainsi qu'un système mécanique permettant la variation de la résistance. Ainsi:
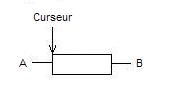
Si vous placez le potentiomètre dans cet état, c'est à dire que le curseur est au plus proche de A, la valeur de la résistance entre A et le curseur est nulle: 0 Ohm.
Par contre en modifiant la position du curseur, pour arriver à cet état là:
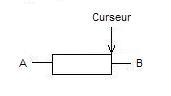
la valeur de la résistance entre A et le curseur est maximale.
Les valeurs maximales de potentiomètre son nombreuses:
- 470 Ohm
- 47 kOhm
- etc.
Organisation des valeurs des résistances
Etant donné la diversité des applications, la précision des valeurs des résistances varie en fonction des dites applications.
C'est la raison pour laquelle la fabrication des résistances est organisée en série à l'intérieure d'une décade.
Série et décade
Une décade est un ensemble de valeurs dont les valeurs de résistance sont comprises entre un multiple de 1 et un multiple de 10 de l'unité considérée.
Exemple : 1 à 10 ohms ; 10 à 100 ohms; 10 à 100 Kohms...
Une série représente le nombre de valeurs différentes que l'on dispose à l'intérieur d'une décade.
Exemples : Pour la série E3 nous avons trois valeurs possibles dans une décade : 1,0 ; 2,2 ; 4,7 .
Soit : 1,0 ohm ; 2,2 ohms ; 4,7 ohms - 10 ohms ; 22 ohms; 47 ohms - 100 ohms - 220 ohms ...
Pour la série E12 nous avons 12 valeurs possibles par décade : 1,0 1,2 1,5 1,8 2,2 2,7 3,3 3,9 4,7 5,6 6,8 8,2 .
Dans la série E12 et pour les résistances dont la valeur est comprise entre 10k et 100k (décade 10k à 100k), nous aurons :
10k 12k 15k 18k 22k 27k 33k 39k 47k 56k 68k 82k.
remarque : la série E12 n'étant plus fabriquée, elle est extraite de la série E24.
La progression des valeurs des résistances
La progression des valeurs dans une série est géométrique.
La valeur de rang m de la série En est obtenue en posant :

Par exemple, 4ème valeur de la série E12 :

Ce qui donne : 2.1544, arrondi à 2,2, qui est aussi le 8ème élément de la série E24 :

Cas spécifique ou n = m
La dernière valeur d'une série sera toujours égale à 10. Nous avons n = m

Dans la pratique nous classerons cette dernière valeur comme valeur de début de chaque décade.
Retrouver une valeur proche dans une série normalisée
Quand on calcule la valeur théorique d'une résistance, lors de la conception d'un circuit électronique, il peut être intéressant de retrouver la valeur pratique de la résistance à mettre en oeuvre dans une série donnée.
Exemple :
Le résultat "x" d'un calcul donne 6,73 ohms comme valeur de résistance.
Quelle est la valeur la plus proche dans la série "n" E24 ?
Il faut d'abord retrouver à quel rang "m" proche appartient cette valeur dans la série E24.
avec :
x = 6,73
n = 24
m = ?
calculons : m = log xn
m= log (6,7324) = 19,87 arrondi à 20.
La valeur la plus proche appartient au rang 20 de la série E24.
soit : 
Précision ou tolérance
En augmentant le nombre de valeurs possibles dans une décade (3, 6, 12, 24, 48, 96), les valeurs de résistance se rapprochent de plus en plus.
Pour obtenir de plus en plus de valeurs proches les unes des autres, les constructeurs ont dû améliorer leurs procédés de fabrication d'une part et employer des matériaux fiables et stables dans le temps d'autre part.
C'est de cette manière que nous avons obtenu des précisions différentes en fonction de la série utilisée.
Tableau des séries normalisées
|